Algèbre relationnelleLes opérateurs bi-relations

Le produit cartésien

Le produit cartésien consiste à prendre deux relations et à faire toutes les associations de tuples possibles entre ces deux relations.

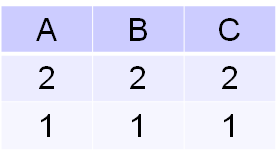
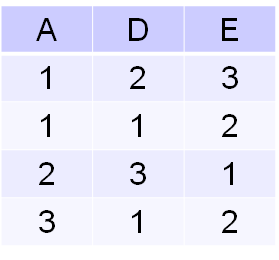
Soient r et s deux relations sur R, r et s n'ont pas forcément le même schéma de relation. Disons par exemple que schéma(r)={A,B,C} tandis que schéma(s)={A,D,E}. r X s aura comme schéma de relation {r.1,r.B,r.C,s.A,s.D,s.E}

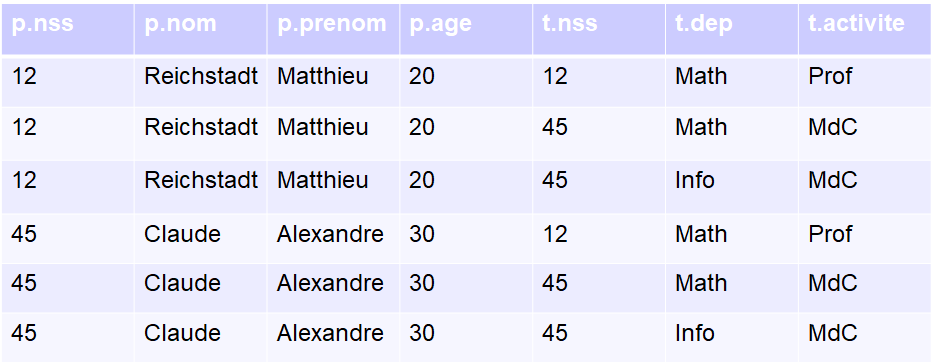
Nous allons essayer de faire un produit cartésien sur notre base:

Personnes X Travaillent

πnom(Personnes)
Ici, on voit qu'on a associé nos 2 tuples de personnes aux 3 tuples de travaillent. On arrivent donc à 2x3=6 tuples dans notre relation finale. A noter que dans le cas des produits cartésiens, comme pour les jointures, on garde tous les attributs, même les attributs de même nom, et on préfixe avec le nom de la relation (ici je n'ai mis que les initiales par souci de place).



La jointure naturelle

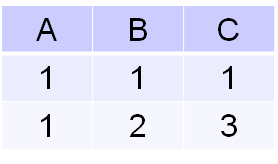
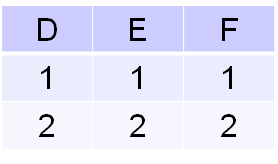
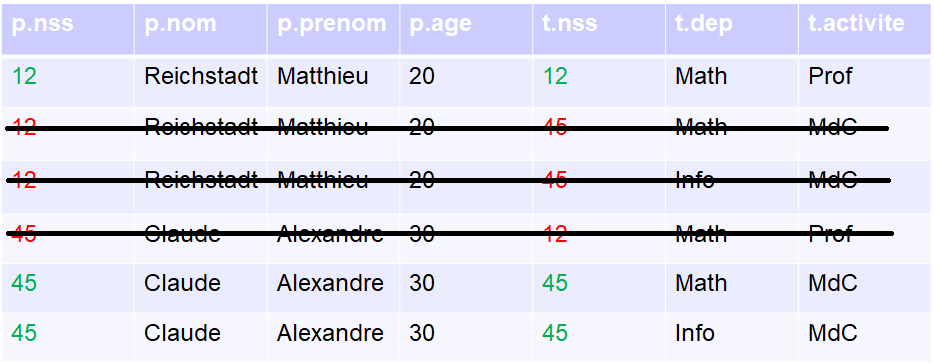
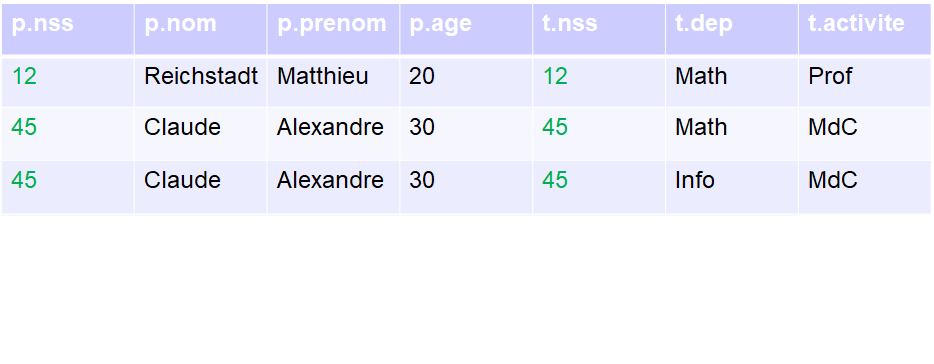
La jointure naturelle reprend a peu près le principe du produit cartésien, mais lui ajoute une petite condition. Cette condition, et bien elle est très basique: si des attributs ont le même nom (ou si la jointure est forcée entre attributs différents), alors ils devront avoir la même valeur dans le tuple pour que ce dernier soit gardé.

Soient r1 et r2 deux relations sur R1 et R2 respectivement.
La jointure naturelle de r1 et r2, notée r1 ∞ r2, est une relation sur un schéma de relation R, avec schema(R) = schema(R1) ∪ schema(R2), définie par : r1 ∞ r2 = {t | ∃ t1 ∈ r1, ∃ t2 ∈ r2 tq t[schema(R1) = t1 et t[schema(R2)]) = t2]}

"Ah ça y est, je suis définitivement perdu! Quelle daube ce cours!"
Mais non! Vous allez voir avec un exemple tout simple vous allez comprendre. Reprenons le résultat du produit cartésien ci-dessus. Si on doit avoir un attribut en commun, ce sera forcément nss, donc pour garder les tuples, il faut que sur la ligne on ait p.nss=t.nss. Simple non? Allez on le fait.

departement ∞ travaillent
Etape de vérification
Etape de nettoyage

Allez je suis sympa, je sais que vous adorez votre professeur de C et l'algorithmique, donc c'est cadeau: 
  1. Resultat = 0
  2. for all t1 ∈ r1 do
  3.     for all t2 ∈ r2 do
  4.         if t1[X] = t2[X] then
  5.             Construire un tuple t tq t[schema(R1)] = t1 et t[schema(R2)] = t2
  6.             Resultat = Resultat ∪ {t} 
  7. retourner Resultat

Pour vous entraîner, voici quelques petites questions à faire:
s1
s2
s3
s4
Donnez-moi s1 ∞ s2, s1 ∞ s3, s1 ∞ s4
Si schema(R1) = schema(R2), que vaut r1 ∞ r2?
Si schema(R1) ∩ schema(R2) = ∅, que vaut r1 ∞ r2?